How to Implement a Binary Heap (Javascript)
After reading this post you will have:
- A high level understanding of the heap data structure.
- Implemented a min-heap in javascript.
The Binary Heap is a more complex data structure to implement from scratch. Having said that, it's widely used in various algorithms such as:
- Graph Traversal
- Sorting
- Path-Finding
For example, Google Maps (which we all know and love) uses some type of a binary heap when calculating the shortest route from point A to B.
What is a Binary Heap?
Think of a binary heap as a pile of tangerines:

When we want to extract a tangerine from the pile, we grab the top one for a couple of reasons:
- If we grab a tangerine from the bottom, the pile would collapse.
- The top element is deemed to be the "most valuable".
As we go down the pile of fruit, the value or priority of the tangerines decreases.
The same idea applies to a binary heap.
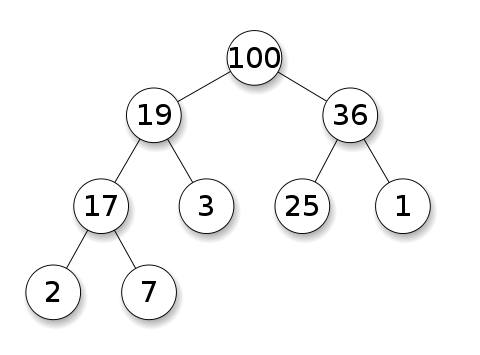
Unlike the pile of fruit, a binary heap consists of nodes that each hold a value which could be a number, a string, or an object.
Each node has a maximum of 2 children (hence the name "binary heap"), but it is possible for a node to have 1 or no children as shown above.
As before, we can only extract the topmost element from the heap, which is considered to be of the "highest priority".
A heap in which all parent nodes are greater than or equal to the children is called a Max-Heap. While a heap in which all parent nodes are less than or equal to the children is called a Min-Heap.
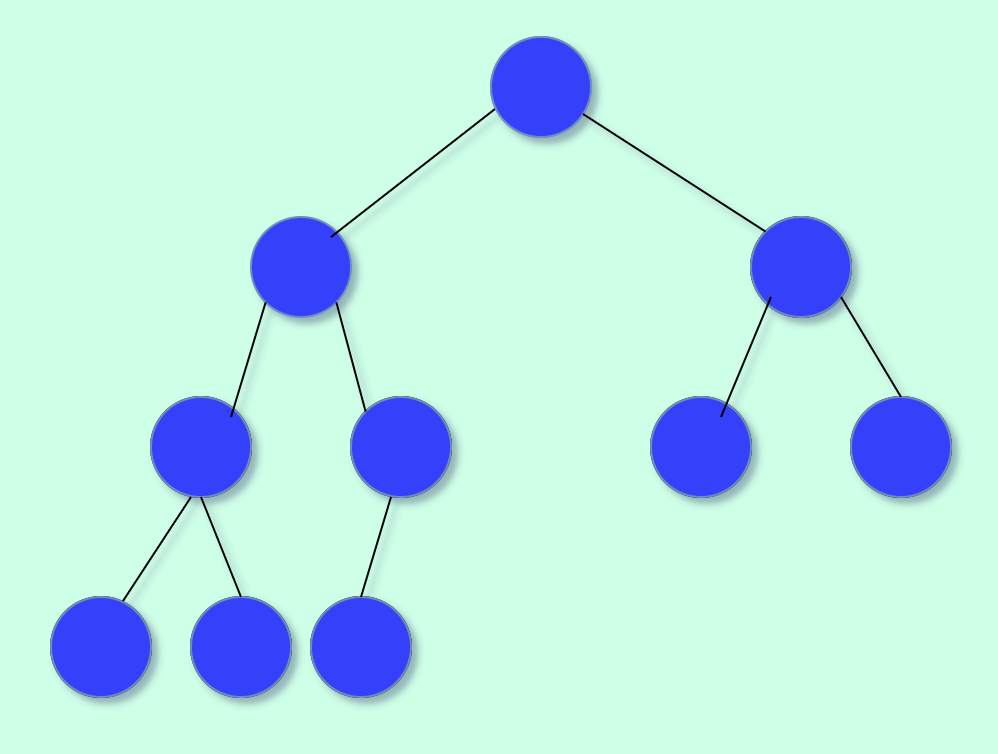
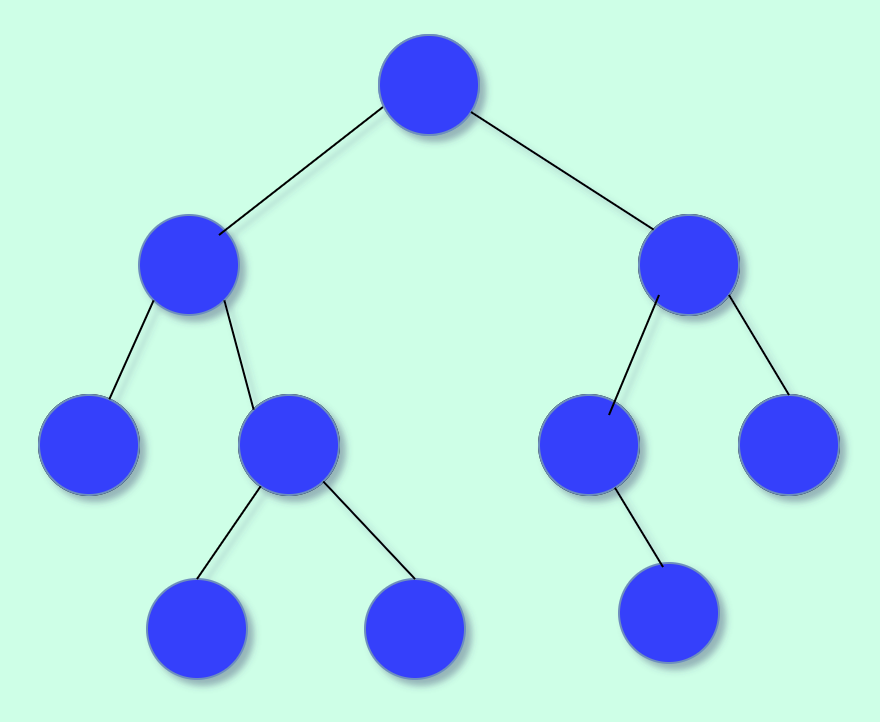
It is important to note that a binary heap should always be a complete binary tree. This means that at every level, except possibly the last, all nodes are completely filled, and all nodes are as far left as possible.
An Example of a complete binary tree:
Example of an incomplete binary tree:
Array Representation of a Tree
The final step before getting into the code is understanding how a tree can be represented using an array.
- The root of the tree will be in position 1 of the array.
- The left child of any given node at position n, will be located at 2n.
- The right child of a node at position n will be located at position 2n + 1.
- The parent of a node at position n is at position n/2.
Array representation of a complete binary tree:
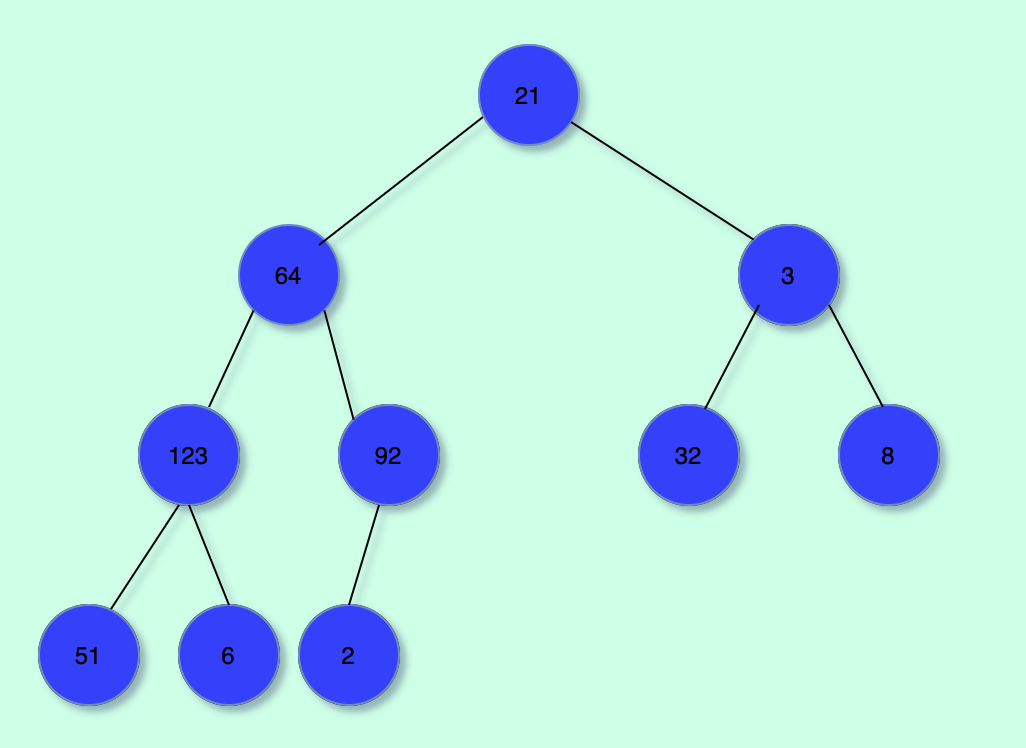
[0 ,21, 64, 3, 123, 92, 32, 8, 51, 6, 2]Tip: A complete binary tree, when represented as an array, will have no null values except for the first element at position 0.
Operations in a Binary Heap
A binary heap should support the following two operations:
- Insert element.
- Extract element.
The Code (Min Heap)
Now that we understand that a binary heap is also complete binary tree. Let's take a closer look at the implementation of the heap operations.
Let's start by defining a javascript class:
export class MinHeap {
constructor(selector) {
this.items = [];
this.selector = selector;
}
push(){}
pop(){}
}In the above code, selector is a function provided by the user that should return the value representation of each element stored in the heap. This is done so that we can later compare the stored elements/objects.
Insert
In a heap, each element is inserted at the element in the tree such that it remains a complete binary tree.
In the array representation, we simply append the new element at the end of the array.
Illustration:
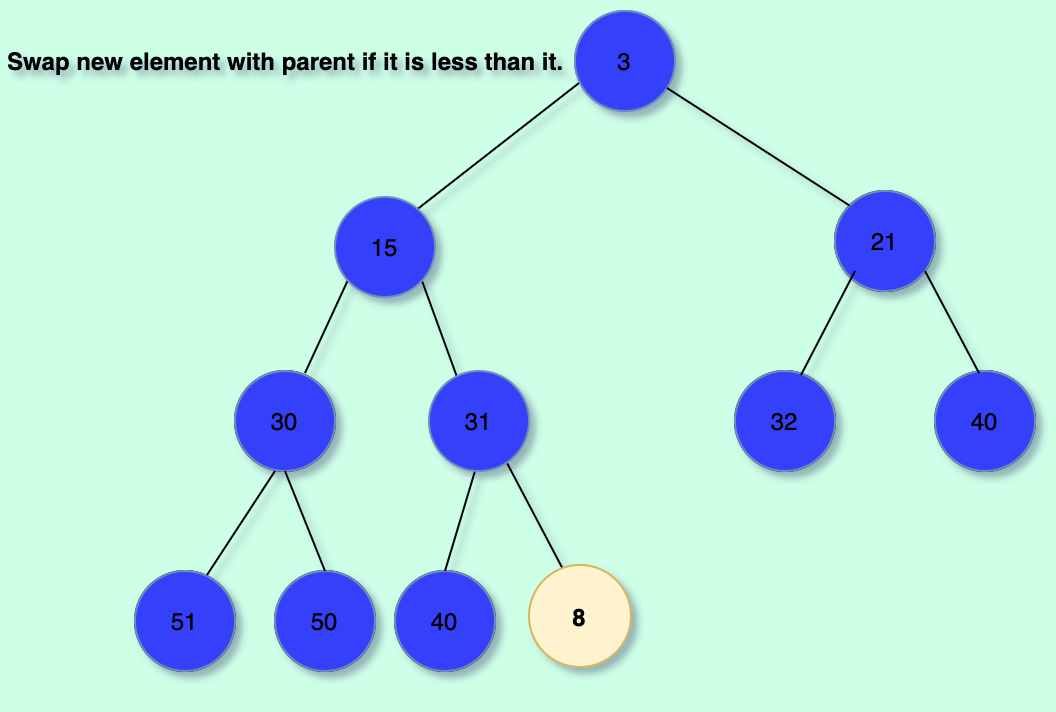
We then proceed to "bubble up" the nodes. This means we simply swap with the parent of the newly inserted node until its parent is less than or equal to it. This conserves our complete binary tree to remain a min-heap.
Illustration:
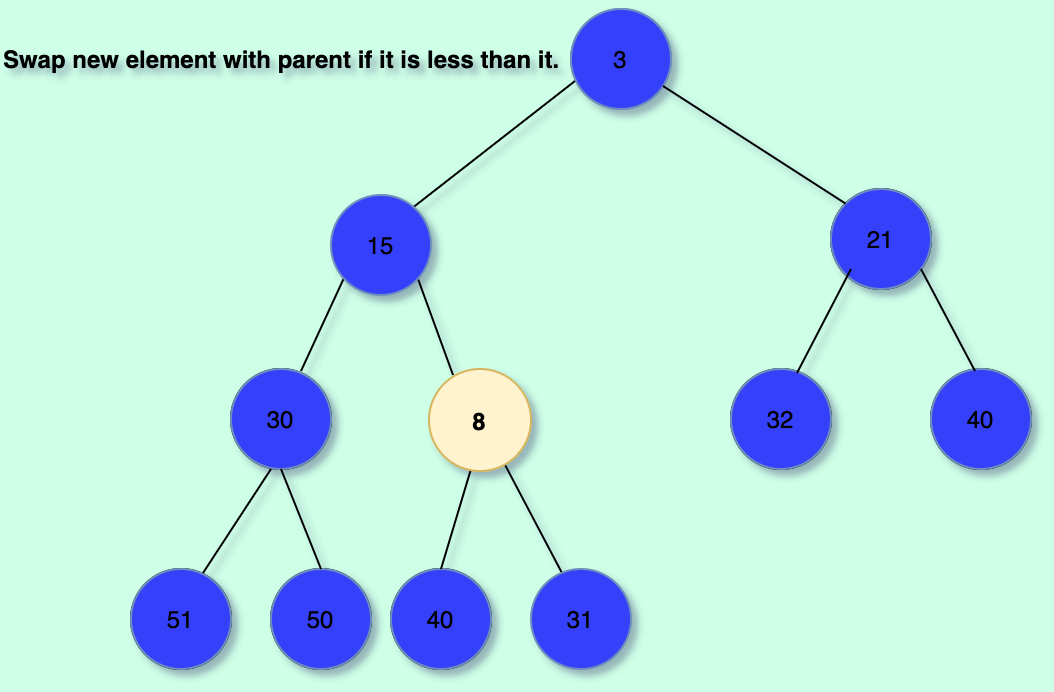
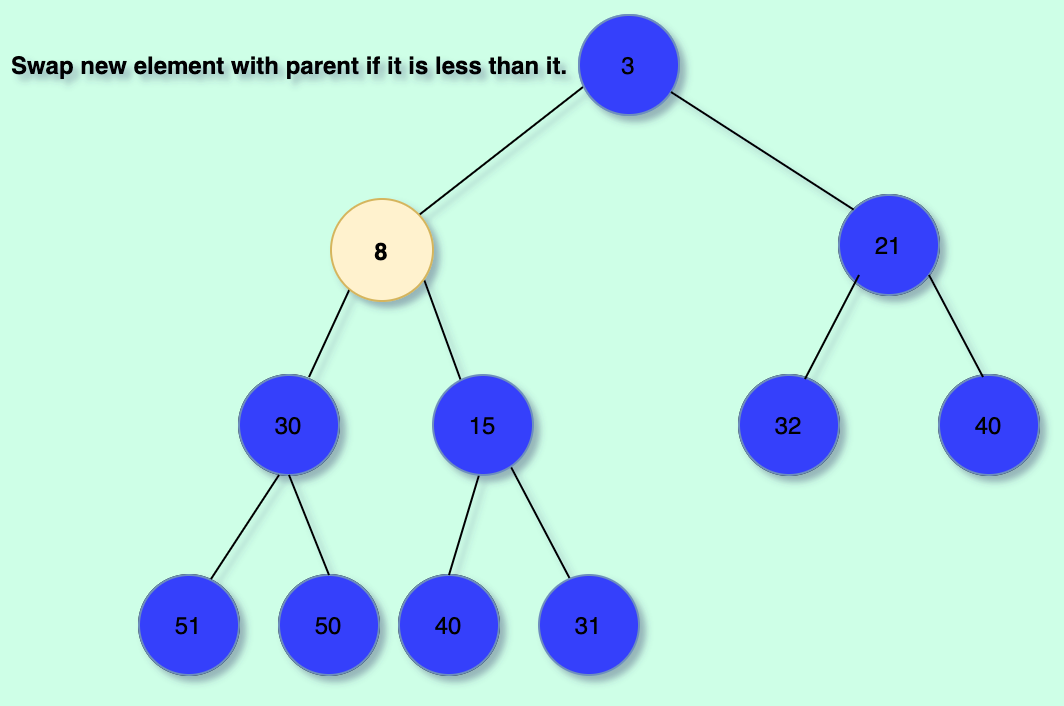
The code:
export class MinHeap {
constructor(selector) {
this.items = [];
this.selector = selector;
}
insert() {
let i = this.items.length;
this.items.push(item);
let parentIndex = Math.floor((i + 1) / 2 - 1);
if (parentIndex < 0) parentIndex = 0;
let parentVal = this.selector(this.items[parentIndex]);
const pushedVal = this.selector(this.items[i]);
while (i > 0 && parentVal > pushedVal) {
parentIndex = Math.floor((i + 1) / 2 - 1);
this.swap(i, parentIndex);
i = parentIndex;
parentVal = this.selector(
this.items[Math.max(Math.floor((i + 1) / 2 - 1), 0)]
);
}
}
}Remove
As mentioned, removing an element from the heap consists in taking the topmost element and then adjusting the heap so that:
- It remains as a complete binary tree.
- It remains a valid min heap.
This is done by placing the last element in the heap as the topmost one and then "bubble it down" in order to conserve the min-heap property.
Step-By-Step Illustration:
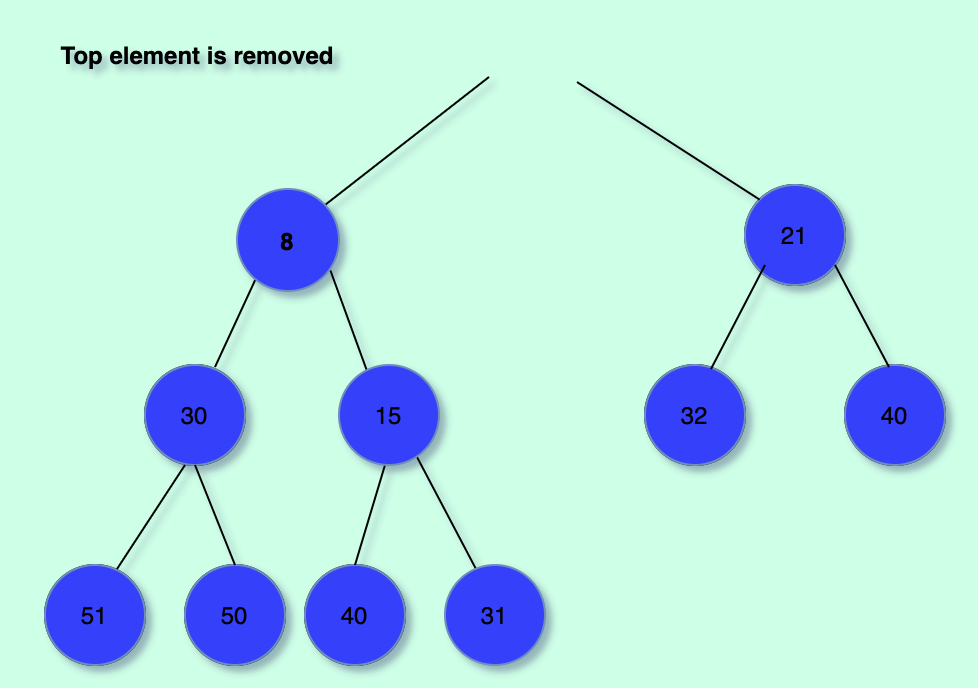
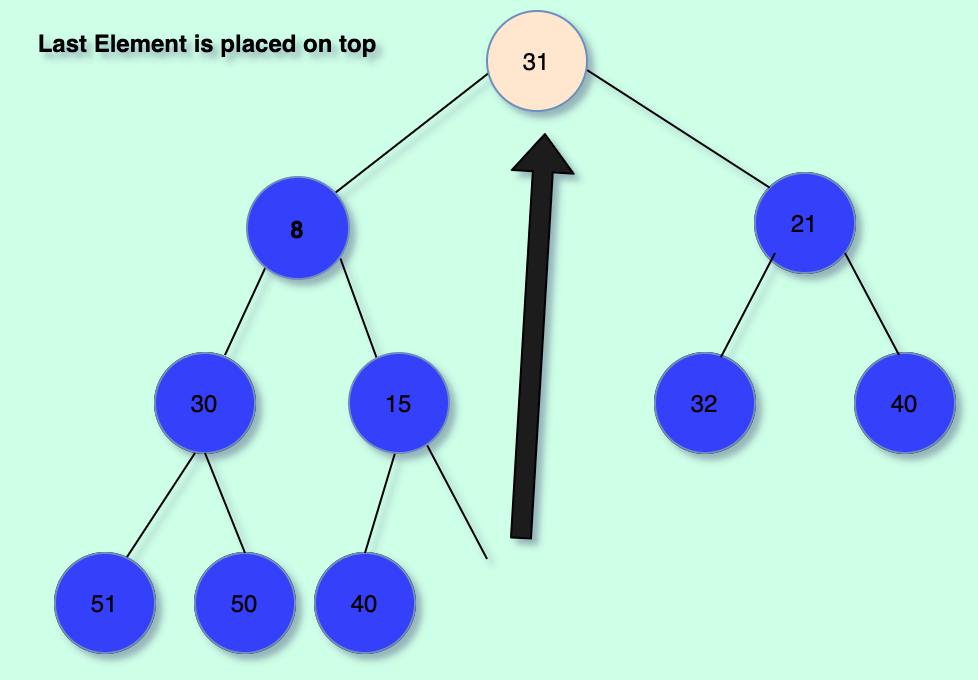
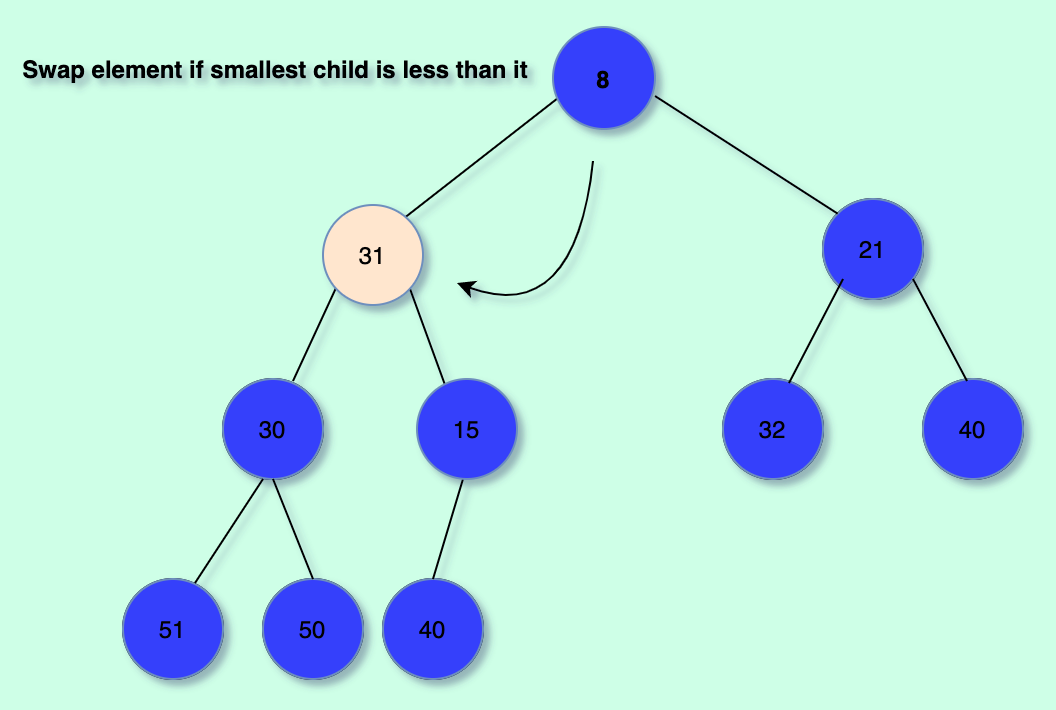
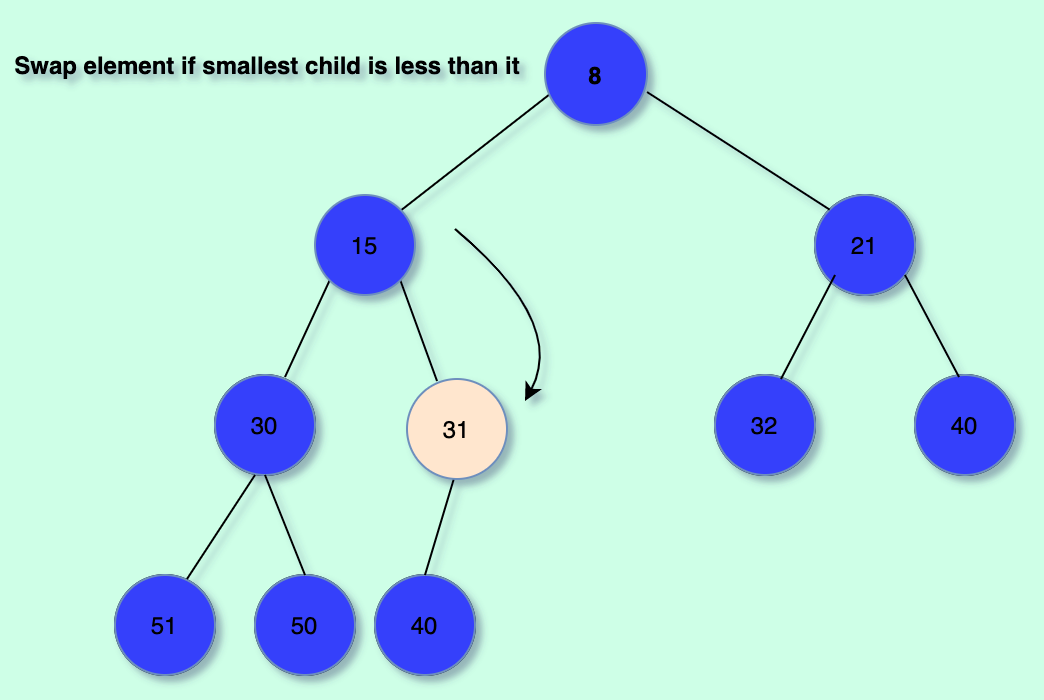
The code:
export class MinHeap {
constructor(selector) {
this.items = [];
this.selector = selector;
}
remove() {
if (this.items.length <= 1) return this.items.pop(); //If it is the last element pop it
const ret = this.items[0]; // What we will return
let temp = this.items.pop();
this.items[0] = temp; // Place last element in array at front
let i = 0; // We adjust heap from top to down
while (true) {
let rightChildIndex = (i + 1) * 2;
let leftChildIndex = (i + 1) * 2 - 1;
let lowest = rightChildIndex;
if (
leftChildIndex >= this.items.length &&
rightChildIndex >= this.items.length
)
break;
if (leftChildIndex >= this.items.length) lowest = rightChildIndex;
if (rightChildIndex >= this.items.length) lowest = leftChildIndex;
if (
!(leftChildIndex >= this.items.length) &&
!(rightChildIndex >= this.items.length)
) {
lowest =
this.selector(this.items[rightChildIndex]) <
this.selector(this.items[leftChildIndex])
? rightChildIndex
: leftChildIndex;
} // Find the smallest child
// If the parent is greater than the smallest child: swap
if (this.selector(this.items[i]) > this.selector(this.items[lowest])) {
this.swap(i, lowest);
i = lowest;
} else break; // We have finished setting up the heap
}
// Return topmost element
return ret;
}
}After this, you may add other operations to satisfy your needs such as: isEmpty(), peek(), etc. These should be straightforward to add.
There you have it! That's a simple implementation of a binary heap in javascript.
If your'e curious of an application that relies heavily on a heap data structure, I built a Online Graph Algorithms Visualization playground you could check out. Link Here